 размера
размера 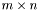 ,
, 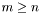 называется ее представление
называется ее представление 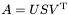 , где
, где
Функции | |
| void | svd_decomp (double **A, size_t m, size_t n, double *w, int matu, double **U, int matv, double **V, size_t *ierr) |
| Сингулярное разложение матрицы. | |
| void | svd_correct (double *w, size_t n, double rel_err) |
| Автоматическое корректирование вычисленных сингулярных чисел. | |
| double | svd_cond (double *w, size_t n) |
| Вычисление спектрального числа обусловленности на основе сингулярного разложения. | |
| void | svd_least_squares (double **U, double *w, double **V, size_t m, size_t n, double *b, double *x) |
| Нахождение нормального псевдорешения системы линейных уравнений на основе сингулярного разложения. | |
Файл содержит функции, строящие и использующие сингулярное разложение матрицы.
Cингулярным разложением прямоугольной матрицы  размера
размера 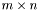 ,
, 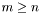 называется ее представление
называется ее представление 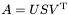 , где
, где
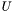 - матрица размера
- матрица размера 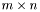 с ортонормированными столбцами,
с ортонормированными столбцами,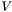 - ортогональная матрица размера
- ортогональная матрица размера 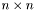 ,
,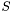 - диагональная
- диагональная 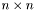 матрица с неотрицательными диагональными элементами, называемыми сингулярными числами.
матрица с неотрицательными диагональными элементами, называемыми сингулярными числами.
Отношение максимального сингулярного числа к минимальному есть спектральное число обусловленности квадратной матрицы. Число 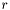 ненулевых сингулярных чисел указывает ранг матрицы. При вычислениях на компьютере вместо нулевых сингулярных чисел могут быть получены ненулевые, поэтому вычисленные сингулярные числа необходимо отредактировать с учетом погрешности вычислений.
ненулевых сингулярных чисел указывает ранг матрицы. При вычислениях на компьютере вместо нулевых сингулярных чисел могут быть получены ненулевые, поэтому вычисленные сингулярные числа необходимо отредактировать с учетом погрешности вычислений.
Сингулярное разложение используется для нахождения нормального псевдорешения прямоугольной системы 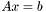 . Вектор x называется псевдорешением системы
. Вектор x называется псевдорешением системы 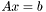 , если на нем достигается минимум
, если на нем достигается минимум 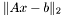 . Псевдорешение
. Псевдорешение 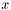 называется нормальным, если среди всех псевдорешений оно имеет минимальную длину. Для любой системы нормальное псевдорешение единственно.
называется нормальным, если среди всех псевдорешений оно имеет минимальную длину. Для любой системы нормальное псевдорешение единственно.
Пусть 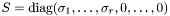 ,
, 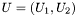 ,
, 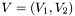 , где
, где 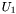 ,
, 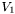 имеют по
имеют по 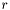 столбцов каждая. Нормальное псевдорешение можно найти по формуле
столбцов каждая. Нормальное псевдорешение можно найти по формуле 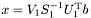 .
.
| double svd_cond | ( | double * | w, | |
| size_t | n | |||
| ) |
Вычисление спектрального числа обусловленности на основе сингулярного разложения.
Функция вычисляет спектральное число обусловленности матрицы  на основе найденного функцией svd_decomp сингулярного разложения
на основе найденного функцией svd_decomp сингулярного разложения 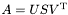 . Матрица A имеет размеры
. Матрица A имеет размеры 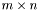 ,
, 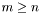 . Спектральное число обусловленности равно отношению максимального сингулярного значения к минимальному.
. Спектральное число обусловленности равно отношению максимального сингулярного значения к минимальному.
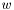 - вектор длины
- вектор длины  , возвращаемый функцией svd_decomp и содержащий сингулярные числа матрицы
, возвращаемый функцией svd_decomp и содержащий сингулярные числа матрицы 
 - число столбцов матрицы
- число столбцов матрицы 
Трудоемкость:
| void svd_correct | ( | double * | w, | |
| size_t | n, | |||
| double | rel_err | |||
| ) |
Автоматическое корректирование вычисленных сингулярных чисел.
Функция зануляет близкие к нулю сингулярные числа матрицы  , вычисленные функцией svd_decomp, с учетом задаваемой относительной погрешности
, вычисленные функцией svd_decomp, с учетом задаваемой относительной погрешности 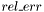 . Матрица A имеет размеры
. Матрица A имеет размеры 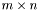 ,
, 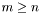 . Величина
. Величина 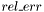 должна отражать ошибку в исходных данных (в матрице
должна отражать ошибку в исходных данных (в матрице  ). Если данные рассматриваются как точные, то необходимо задать
). Если данные рассматриваются как точные, то необходимо задать 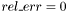 . В этом случае функция установит значение
. В этом случае функция установит значение 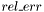 , отражающее ошибку при вычислениях в самой функции svd_decomp, а именно,
, отражающее ошибку при вычислениях в самой функции svd_decomp, а именно, 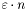 , где
, где 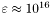 - расстояние между
- расстояние между 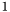 и следующим за ним числом в арифметике двойной точности. Зануляются сингулярные значения, не превосходящие
и следующим за ним числом в арифметике двойной точности. Зануляются сингулярные значения, не превосходящие 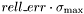 , где
, где 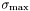 - максимальное сингулярное значение.
- максимальное сингулярное значение.
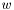 - вектор длины n, возвращаемый функцией svd_decomp.
- вектор длины n, возвращаемый функцией svd_decomp. - число столбцов матрицы A
- число столбцов матрицы A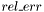 - относительная погрешность
- относительная погрешность
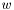 - скорректированные сингулярные числа, вектор длины
- скорректированные сингулярные числа, вектор длины 
| void svd_decomp | ( | double ** | A, | |
| size_t | m, | |||
| size_t | n, | |||
| double * | w, | |||
| int | matu, | |||
| double ** | U, | |||
| int | matv, | |||
| double ** | V, | |||
| size_t * | ierr | |||
| ) |
Сингулярное разложение матрицы.
Функция находит сингулярное разложение 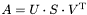 вещественной матрицы A размера
вещественной матрицы A размера 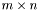 ,
, 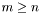 .
.
 - прямоугольная матрица размера
- прямоугольная матрица размера 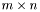
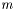 - число строк матрицы
- число строк матрицы 
 - число столбцов матрицы
- число столбцов матрицы 
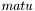 - равно
- равно 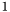 , если требуется найти матрицу
, если требуется найти матрицу 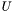 : равно
: равно 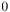 , если не требуется
, если не требуется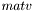 - равно
- равно 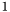 , если требуется найти матрицу
, если требуется найти матрицу 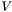 : равно
: равно 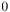 , если не требуется
, если не требуется
 - не изменяется
- не изменяется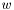 - вектор длины n, содержащий сингулярные числа матрицы
- вектор длины n, содержащий сингулярные числа матрицы  . Числа, обычно (но не обязательно), упорядочены по убыванию. В случае ошибки сингулярные числа, стоящие на позициях
. Числа, обычно (но не обязательно), упорядочены по убыванию. В случае ошибки сингулярные числа, стоящие на позициях 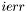 ,
, 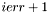 ,
, 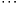 ,
, 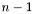 , правильные.
, правильные.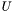 - прямоугольная матрица размера
- прямоугольная матрица размера 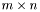 . В случае ошибки столбцы матрицы
. В случае ошибки столбцы матрицы 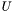 , стоящие на позициях
, стоящие на позициях 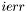 ,
, 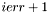 ,
, 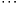 ,
, 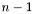 , корректны.
, корректны.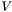 - квадратная матрица порядка
- квадратная матрица порядка  . В случае ошибки столбцы матрицы
. В случае ошибки столбцы матрицы 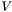 , стоящие на позициях
, стоящие на позициях 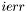 ,
, 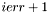 ,
, 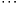 ,
, 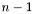 , корректны.
, корректны.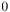 при нормальной работе
при нормальной работе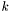 , если
, если 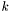 -е сингулярное число не было определено за
-е сингулярное число не было определено за 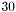 итераций
итераций
Алгоритм состоит из двух частей. На первом этапе отражениями Хаусхолдера матрица  приводится к двухдиагональному виду. На втором этапе вариантом
приводится к двухдиагональному виду. На втором этапе вариантом  -алгоритма двухдиагональная матрица приводится к диагональному виду
-алгоритма двухдиагональная матрица приводится к диагональному виду 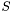 .
.
Функция является переводом фортрановской программы svd из книги [FMM].
Трудоемкость:
Дополнительная память: O(n)
| void svd_least_squares | ( | double ** | U, | |
| double * | w, | |||
| double ** | V, | |||
| size_t | m, | |||
| size_t | n, | |||
| double * | b, | |||
| double * | x | |||
| ) |
Нахождение нормального псевдорешения системы линейных уравнений на основе сингулярного разложения.
Функция находит нормальное псевдорешение системы линейных уравнений 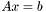 на основе вычисленного функцией svd_decomp сингулярного разложения
на основе вычисленного функцией svd_decomp сингулярного разложения 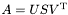 . Матрица A имеет размеры
. Матрица A имеет размеры 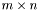 ,
, 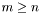 . При вычислении псевдорешения используются только ненулевые сингулярные значения. Перед вызовом функции рекомендуется занулить близкие к нулю сингулярные значения (например, с помощью функции svd_correct).
. При вычислении псевдорешения используются только ненулевые сингулярные значения. Перед вызовом функции рекомендуется занулить близкие к нулю сингулярные значения (например, с помощью функции svd_correct).
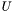 - прямоугольная матрица размера
- прямоугольная матрица размера 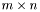 , возвращаемая функцией svd_decomp.
, возвращаемая функцией svd_decomp.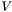 - квадратная матрица порядка
- квадратная матрица порядка  , возвращаемая функцией svd_decomp.
, возвращаемая функцией svd_decomp.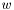 - вектор длины
- вектор длины  , возвращаемый функцией svd_decomp.
, возвращаемый функцией svd_decomp.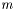 - число строк матрицы
- число строк матрицы 
 - число столбцов матрицы
- число столбцов матрицы 
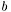 - правая часть системы
- правая часть системы 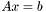 , вектор длины
, вектор длины 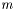
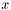 - найденное нормальное псевдорешение, вектор длины
- найденное нормальное псевдорешение, вектор длины 
Трудоемкость:
 1.4.7
1.4.7