Функции
 -разложение матрицы.
-разложение матрицы.  -разложение матрицы, в отличие от qr_decomp работает с транспонированной матрицей.
-разложение матрицы, в отличие от qr_decomp работает с транспонированной матрицей.  -разложения.
-разложения.  -разложения, в отличие от qr_least_unpack работает с транспонированной матрицей.
-разложения, в отличие от qr_least_unpack работает с транспонированной матрицей.  -разложение. Подробнее...
-разложение. Подробнее...
Функции | |
| void | qr_decomp (double **A, size_t m, size_t n, double *t) |
 -разложение матрицы. -разложение матрицы. | |
| void | qr_decomp_t (double **At, size_t m, size_t n, double *t) |
 -разложение матрицы, в отличие от qr_decomp работает с транспонированной матрицей. -разложение матрицы, в отличие от qr_decomp работает с транспонированной матрицей. | |
| void | qr_solve (double **QR, size_t n, double *t, double *b) |
| Решение системы линейных уравнений. | |
| void | qr_solve_t (double **QRt, size_t n, double *t, double *b) |
| Решение системы линейных уравнений, в отличие от qr_solve работает с транспонированной матрицей. | |
| void | qr_least_squares (double **QR, size_t m, size_t n, double *t, double *b, double *r) |
| `Решение' переопределенной системы методом наименьших квадратов. | |
| void | qr_least_squares_t (double **QRt, size_t m, size_t n, double *t, double *b, double *r) |
| `Решение' переопределенной системы методом наименьших квадратов, в отличие от qr_least_squares работает с транспонированной матрицей. | |
| void | qr_least_unpack (double **QR, size_t m, size_t n, double *t, double **Q, double **R) |
Полное представление  -разложения. -разложения. | |
| void | qr_least_unpack_t (double **QRt, size_t m, size_t n, double *t, double **Q, double **R) |
Полное представление  -разложения, в отличие от qr_least_unpack работает с транспонированной матрицей. -разложения, в отличие от qr_least_unpack работает с транспонированной матрицей. | |
 -разложение.
-разложение.
Файл содержит функции, реализующие и использующие  -разложение матрицы.
-разложение матрицы.
Произвольная 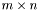 матрица
матрица  ранга
ранга  допускает разложение вида
допускает разложение вида 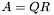 , где
, где 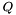 -
- 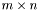 матрица с ортогональными столбцами,
матрица с ортогональными столбцами, 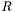 - верхнетреугольная
- верхнетреугольная 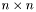 матрица. Такое разложение можно использовать для решения системы линейных уравнений
матрица. Такое разложение можно использовать для решения системы линейных уравнений 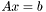 , сводя ее к треугольной системе
, сводя ее к треугольной системе 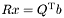 . Данная треугольная система позволяет также найти псевдорешение (в смысле метода наименьших квадратов) переопределенной системы.
. Данная треугольная система позволяет также найти псевдорешение (в смысле метода наименьших квадратов) переопределенной системы.  -разложение используется также для нахождения ортонормированного базиса подпространства. Если
-разложение используется также для нахождения ортонормированного базиса подпространства. Если  имеет полный столбцовый ранг, то столбцы матрицы
имеет полный столбцовый ранг, то столбцы матрицы 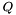 составляют ортонормированный базис подпространства, натянутого на столбцы матрицы
составляют ортонормированный базис подпространства, натянутого на столбцы матрицы  .
.
 -разложения, предпочтительней сначала транспонировать матрицу, а затем использовать функции второго типа.
-разложения, предпочтительней сначала транспонировать матрицу, а затем использовать функции второго типа. | void qr_decomp | ( | double ** | A, | |
| size_t | m, | |||
| size_t | n, | |||
| double * | t | |||
| ) |
 -разложение матрицы.
-разложение матрицы.
Функция находит  -разложение
-разложение 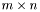 матрицы A ранга
матрицы A ранга  . На выходе диагональ и верхнетреугольная часть матрицы
. На выходе диагональ и верхнетреугольная часть матрицы  содержат элементы матрицы
содержат элементы матрицы 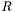 . Матрица
. Матрица 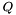 представлена элементами ниже диагонали и вектором
представлена элементами ниже диагонали и вектором 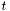 . Вектор
. Вектор 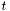 имеет длину
имеет длину  . Матрица
. Матрица 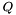 определяется произведением матриц отражений Хаусхолдера:
определяется произведением матриц отражений Хаусхолдера: 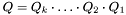 , где
, где 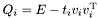 и
и 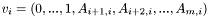 . Такая же схема используется в библиотеках LAPACK, GSL и др.
. Такая же схема используется в библиотеках LAPACK, GSL и др.
Для разложения используется алгоритм вращений Хаусхолдера (См. [GolubVanLoan], алгоритм 5.2.1).
 - матрица,
- матрица,  -разложение которой требуется найти
-разложение которой требуется найти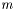 ,
,  - размеры матрицы A
- размеры матрицы A ,
, 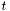 - матрица и вектор, которые задают
- матрица и вектор, которые задают  -разложение исходной матрицы
-разложение исходной матрицы
Трудоемкость: 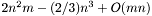
| void qr_decomp_t | ( | double ** | At, | |
| size_t | m, | |||
| size_t | n, | |||
| double * | t | |||
| ) |
 -разложение матрицы, в отличие от qr_decomp работает с транспонированной матрицей.
-разложение матрицы, в отличие от qr_decomp работает с транспонированной матрицей.
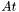 - матрица,
- матрица,  -разложение которой требуется найти
-разложение которой требуется найти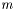 ,
,  - размеры матрицы
- размеры матрицы 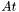
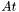 ,
, 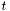 - матрица и вектор, которые задают
- матрица и вектор, которые задают  -разложение исходной матрицы
-разложение исходной матрицы
Трудоемкость: 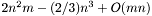
| void qr_least_squares | ( | double ** | QR, | |
| size_t | m, | |||
| size_t | n, | |||
| double * | t, | |||
| double * | b, | |||
| double * | r | |||
| ) |
`Решение' переопределенной системы методом наименьших квадратов.
Функция находит псевдорешение переопределенной 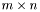 системы линейных уравнений
системы линейных уравнений 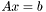 ранга
ранга  , используя предварительно найденное
, используя предварительно найденное  -разложение матрицы
-разложение матрицы  .
.  -разложение должно быть представлено матрицей
-разложение должно быть представлено матрицей  и вектором
и вектором 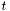 , возвращаемыми функцией qr_decomp. Псевдорешение минимизирует евклидову норму невязки
, возвращаемыми функцией qr_decomp. Псевдорешение минимизирует евклидову норму невязки 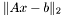 . Псевдорешение
. Псевдорешение 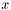 записывается на месте вектора правой части
записывается на месте вектора правой части 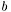 . Невязка
. Невязка 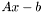 возвращается в векторе
возвращается в векторе 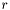 .
.
Трудоемкость: 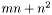
| void qr_least_squares_t | ( | double ** | QRt, | |
| size_t | m, | |||
| size_t | n, | |||
| double * | t, | |||
| double * | b, | |||
| double * | r | |||
| ) |
`Решение' переопределенной системы методом наименьших квадратов, в отличие от qr_least_squares работает с транспонированной матрицей.
Функция находит псевдорешение переопределенной 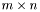 системы линейных уравнений
системы линейных уравнений 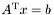 , используя предварительно найденное
, используя предварительно найденное  -разложение матрицы
-разложение матрицы 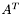 .
.  -разложение должно быть представлено матрицей
-разложение должно быть представлено матрицей  и вектором
и вектором 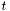 , возвращаемыми функцией qr_decomp_t. Псевдорешение минимизирует евклидову норму невязки
, возвращаемыми функцией qr_decomp_t. Псевдорешение минимизирует евклидову норму невязки 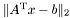 . Псевдорешение
. Псевдорешение 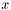 записывается на месте вектора правой части
записывается на месте вектора правой части 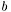 . Невязка
. Невязка 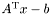 возвращается в векторе
возвращается в векторе 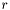 .
.
Трудоемкость: 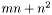
| void qr_least_unpack | ( | double ** | QR, | |
| size_t | m, | |||
| size_t | n, | |||
| double * | t, | |||
| double ** | Q, | |||
| double ** | R | |||
| ) |
Полное представление  -разложения.
-разложения.
Функция находит матрицы 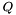 ,
, 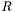 размеров
размеров 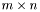 и
и 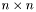 соответственно, представленные в запакованном формате
соответственно, представленные в запакованном формате  ,
, 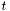 .
.
Трудоемкость:
| void qr_least_unpack_t | ( | double ** | QRt, | |
| size_t | m, | |||
| size_t | n, | |||
| double * | t, | |||
| double ** | Q, | |||
| double ** | R | |||
| ) |
Полное представление  -разложения, в отличие от qr_least_unpack работает с транспонированной матрицей.
-разложения, в отличие от qr_least_unpack работает с транспонированной матрицей.
Функция находит матрицы Q, R размеров 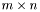 и
и 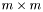 соответственно, представленные в запакованном формате
соответственно, представленные в запакованном формате  ,
, 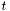 .
.
Трудоемкость:
| void qr_solve | ( | double ** | QR, | |
| size_t | n, | |||
| double * | t, | |||
| double * | b | |||
| ) |
Решение системы линейных уравнений.
Функция находит решение квадратной системы линейных уравнений 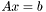 порядка
порядка  . Функция использует предварительно найденное
. Функция использует предварительно найденное  -разложение матрицы
-разложение матрицы  , представленное матрицей
, представленное матрицей  и вектором
и вектором 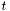 , которые возвращаются функцией qr_decomp. Решение
, которые возвращаются функцией qr_decomp. Решение 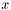 записывается на месте вектора правой части
записывается на месте вектора правой части 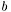 . Матрица
. Матрица  и вектор
и вектор 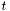 не меняются данной функцией и могут быть использованы для решения системы с другой правой частью.
не меняются данной функцией и могут быть использованы для решения системы с другой правой частью.
Используется алгоритм прямой и обратной подстановки.
Трудоемкость: 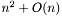
| void qr_solve_t | ( | double ** | QRt, | |
| size_t | n, | |||
| double * | t, | |||
| double * | b | |||
| ) |
Решение системы линейных уравнений, в отличие от qr_solve работает с транспонированной матрицей.
Функция находит решение квадратной системы линейных уравнений 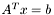 порядка
порядка  . Функция использует предварительно найденное
. Функция использует предварительно найденное  -разложение матрицы
-разложение матрицы  , представленное матрицей
, представленное матрицей  и вектором
и вектором 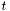 , которые возвращаются функцией qr_decomp_t. Решение
, которые возвращаются функцией qr_decomp_t. Решение 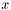 записывается на месте вектора правой части
записывается на месте вектора правой части 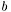 . Матрица
. Матрица  и вектор
и вектор 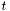 не меняются данной функцией и могут быть использованы для решения системы с другой правой частью.
не меняются данной функцией и могут быть использованы для решения системы с другой правой частью.
Используется алгоритм прямой и обратной подстановки.
Трудоемкость: 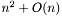
 1.4.7
1.4.7