Функции
 -разложение матрицы.
-разложение матрицы.  , представленной массивами
, представленной массивами  и
и 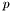 , на вектор
, на вектор 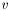 .
.  -разложение. Подробнее...
-разложение. Подробнее...
Функции | |
| double | lu_decomp (double **A, size_t n, size_t *p, int *sgn) |
 -разложение матрицы. -разложение матрицы. | |
| void | lu_solve (double **LU, size_t n, size_t *p, double *b) |
| Решение системы линейных уравнений. | |
| void | lu_improve (double **LU, size_t n, size_t *p, double *b, double *x, double *r) |
| Один шаг итерационного уточнения решения системы линейных уравнений. | |
| double | lu_det (double **LU, size_t n, int sgn) |
| Определитель матрицы. | |
| void | lu_invert (double **LU, size_t n, size_t *p, double **B) |
| Обращение матрицы. | |
| void | lu_mult_col (double **LU, size_t n, size_t *p, double *v, double *res) |
Умножение матрицы  , представленной массивами , представленной массивами  и и 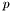 , на вектор , на вектор 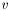 . . | |
 -разложение.
-разложение.
Файл содержит функции, реализующие и использующие  -разложение квадратной матрицы.
-разложение квадратной матрицы.
Произвольная квадратная матрица  порядка
порядка  допускает разложение вида
допускает разложение вида 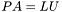 , где
, где 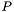 - матрица перестановок,
- матрица перестановок, 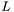 - нижнетреугольная матрица с единичной диагональю,
- нижнетреугольная матрица с единичной диагональю, 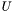 - верхнетреугольная матрица. Такое разложение используют для решения систем линейных уравнений
- верхнетреугольная матрица. Такое разложение используют для решения систем линейных уравнений 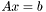 , заменяя данную систему на пару систем
, заменяя данную систему на пару систем 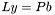 и
и 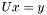 .
.
| double lu_decomp | ( | double ** | A, | |
| size_t | n, | |||
| size_t * | p, | |||
| int * | sgn | |||
| ) |
 -разложение матрицы.
-разложение матрицы.
Функция находит  -разложение и оценку числа обусловленности квадратной матрицы
-разложение и оценку числа обусловленности квадратной матрицы  порядка
порядка  . На выходе диагональ и верхнетреугольная часть матрицы
. На выходе диагональ и верхнетреугольная часть матрицы  содержат элементы матрицы
содержат элементы матрицы 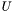 . Нижнетреугольная часть матрицы
. Нижнетреугольная часть матрицы  содержит поддиагональные элементы матрицы
содержит поддиагональные элементы матрицы 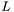 . Диагональные элементы матрицы
. Диагональные элементы матрицы 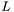 равны
равны 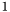 . Матрица перестановок
. Матрица перестановок 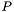 представлена вектором перестановок
представлена вектором перестановок 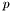 , в котором
, в котором ![$p[j]$](form_140.png) - индекс ведущей строки на
- индекс ведущей строки на 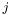 -ой итерации. На выходе
-ой итерации. На выходе 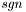 - определитель матрицы
- определитель матрицы 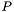 . Функция возвращает нижнюю оценку числа обусловленности матрицы
. Функция возвращает нижнюю оценку числа обусловленности матрицы  порядка
порядка  . Как правило, данная оценка отличается от настоящего числа обусловленности не более чем в
. Как правило, данная оценка отличается от настоящего числа обусловленности не более чем в 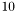 раз.
раз.
Для разложения используется алгоритм Гаусса с выбором главного элемента по столбцу. Для оценки числа обусловленности используется алгоритм, описанный в [FMM, KMN].
Трудоемкость: 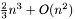 операций с плавающей запятой
операций с плавающей запятой
| double lu_det | ( | double ** | LU, | |
| size_t | n, | |||
| int | sgn | |||
| ) |
Определитель матрицы.
Функция возвращает определитель квадратной матрицы  порядка
порядка  . Ииспользуется предварительно найденное
. Ииспользуется предварительно найденное  -разложение матрицы A, представленное матрицей
-разложение матрицы A, представленное матрицей  и определителем
и определителем 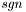 матрицы перестановок
матрицы перестановок 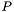 (сам вектор перестановок не нужен), возвращаемыми функцией lu_decomp.
(сам вектор перестановок не нужен), возвращаемыми функцией lu_decomp.
Трудоемкость: 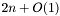 операций с плавающей запятой
операций с плавающей запятой
| void lu_improve | ( | double ** | LU, | |
| size_t | n, | |||
| size_t * | p, | |||
| double * | b, | |||
| double * | x, | |||
| double * | r | |||
| ) |
Один шаг итерационного уточнения решения системы линейных уравнений.
Функция выполняет один шаг итерационного уточнения решения 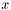 системы линейных уравнений
системы линейных уравнений 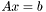 . Используется предварительно найденное
. Используется предварительно найденное  -разложение матрицы
-разложение матрицы  , представленное матрицей
, представленное матрицей  и вектором перестановок
и вектором перестановок 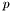 , возвращаемыми функцией lu_decomp. Возвращается улучшенное решение
, возвращаемыми функцией lu_decomp. Возвращается улучшенное решение 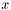 и вектор невязки
и вектор невязки 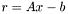 .
.
Используется следующий алгоритм: вначале вычисляется вектор 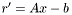 , после этого с помощью функции lu_solve решается система
, после этого с помощью функции lu_solve решается система 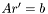 и, наконец, определяется улучшенное решение
и, наконец, определяется улучшенное решение 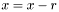 и вектор невязки
и вектор невязки 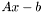 .
.
Трудоемкость: 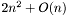 операций с плавающей запятой
операций с плавающей запятой
| void lu_invert | ( | double ** | LU, | |
| size_t | n, | |||
| size_t * | p, | |||
| double ** | B | |||
| ) |
Обращение матрицы.
Функция находит матрицу 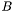 , обратную к матрице
, обратную к матрице  . Используется предварительно найденное
. Используется предварительно найденное  -разложение матрицы
-разложение матрицы  , представленное матрицей
, представленное матрицей  и вектором перестановок
и вектором перестановок 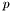 , возвращаемыми функцией lu_decomp.
, возвращаемыми функцией lu_decomp.
Трудоемкость: 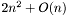 операций с плавающей запятой
операций с плавающей запятой
| void lu_mult_col | ( | double ** | LU, | |
| size_t | n, | |||
| size_t * | p, | |||
| double * | v, | |||
| double * | res | |||
| ) |
Умножение матрицы  , представленной массивами
, представленной массивами  и
и 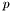 , на вектор
, на вектор 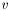 .
.
Функция находит произведение 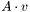 . Используется предварительно найденное
. Используется предварительно найденное  -разложение матрицы
-разложение матрицы  , представленное матрицей
, представленное матрицей  и вектором перестановок
и вектором перестановок 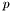 , возвращаемыми функцией lu_decomp. Результат возвращается в векторе
, возвращаемыми функцией lu_decomp. Результат возвращается в векторе 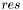 .
.
Трудоемкость: 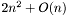 операций с плавающей запятой
операций с плавающей запятой
| void lu_solve | ( | double ** | LU, | |
| size_t | n, | |||
| size_t * | p, | |||
| double * | b | |||
| ) |
Решение системы линейных уравнений.
Функция находит решение квадратной системы линейных уравнений 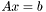 порядка
порядка  , используя предварительно найденное
, используя предварительно найденное  -разложение матрицы
-разложение матрицы  , представленное матрицей
, представленное матрицей  и вектором перестановок
и вектором перестановок 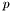 , возвращаемыми функцией lu_decomp. Решение
, возвращаемыми функцией lu_decomp. Решение 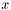 записывается на месте вектора правой части
записывается на месте вектора правой части 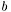 . Матрица
. Матрица 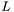 U и вектор
U и вектор 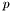 не меняются данной функцией и могут быть использованы для решения системы с другой правой частью.
не меняются данной функцией и могут быть использованы для решения системы с другой правой частью.
Используется алгоритм прямой и обратной подстановки.
Трудоемкость: 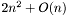 операций с плавающей запятой
операций с плавающей запятой
 1.4.7
1.4.7