Функции
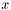 длины
длины  .
. 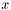 длины
длины  .
.
Функции | |
| void | fft_transform (double *re, double *im, size_t n) |
Прямое быстрое преобразование Фурье для вектора 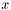 длины длины  . . | |
| void | fft_inverse (double *re, double *im, size_t n) |
Обратное быстрое преобразование Фурье для вектора 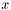 длины длины  . . | |
(Прямым) дискретным преобразованием Фурье называют отображение 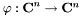 , ставящее в соответствие вектору
, ставящее в соответствие вектору 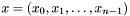 вектор
вектор 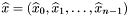 , где
, где 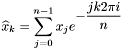
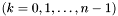 .
.
Обратное отображение 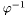 называется обратным дискретным преобразованием Фурье. Его можно вычислить по формулам
называется обратным дискретным преобразованием Фурье. Его можно вычислить по формулам 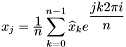
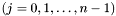 .
.
Быстрое преобразование Фурье - это эффективный способ вычисления прямого и обратного преобразований Фурье. В библиотеке реализован алгоритм быстрого преобразования Фурье для случая, когда  - степень двойки. Чтобы использовать функции для векторов другой длины, необходимо дописать к векторам нулевые компоненты.
- степень двойки. Чтобы использовать функции для векторов другой длины, необходимо дописать к векторам нулевые компоненты.
| void fft_inverse | ( | double * | re, | |
| double * | im, | |||
| size_t | n | |||
| ) |
Обратное быстрое преобразование Фурье для вектора 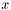 длины
длины  .
.
Действительные части вектора 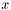 задаются в массиве
задаются в массиве 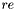 , мнимые части - в массиве
, мнимые части - в массиве 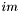 ,
,  должно быть степенью двойки. Результат возвращается в векторах
должно быть степенью двойки. Результат возвращается в векторах 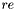 и
и 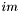 .
.
| void fft_transform | ( | double * | re, | |
| double * | im, | |||
| size_t | n | |||
| ) |
Прямое быстрое преобразование Фурье для вектора 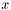 длины
длины  .
.
Действительные части вектора 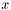 задаются в массиве
задаются в массиве 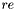 , мнимые части - в массиве
, мнимые части - в массиве 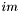 ,
,  должно быть степенью двойки. Результат возвращается в векторах
должно быть степенью двойки. Результат возвращается в векторах 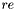 и
и 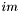 .
.
 1.4.7
1.4.7