|
Функции |
| void | eig_tridiag_reduction (double **A, size_t n, int matq, double *d, double *a) |
| | Приведение симметричной матрицы к трехдиагональному виду.
|
| void | eig_tridiag (double *d, double *a, size_t n, int matq, double **Q, size_t *rc) |
| | Собственные числа симметричной трехдиагональной системы.
|
| void | eig_jacobi (double **A, size_t n, double *w, int matq, double **Q, int *nrot, int *rc) |
| | Метод Якоби решения симметричной проблемы собственных значений.
|
| void | eig_balance (double **A, size_t n, size_t *low, size_t *high, double *scal) |
| | Балансирование вещественной матрицы.
|
| void | eig_hess_reduction (double **A, size_t n, size_t low, size_t high, size_t *perm) |
| | Приведение матрицы к верхней форме Хессенберга.
|
| void | eig_hess_transform_matrix (double **A, size_t n, size_t low, size_t high, size_t *perm, double **Q) |
| | Трансформирующая матрица к верхней форме Хессенберга.
|
| void | eig_hess (double **A, size_t n, size_t low, size_t high, double *wr, double *wi, int matq, double **Q, size_t *iter, size_t *rc) |
| | Собственные числа и векторы матрицы Хессенберга.
|
| void | eig_balance_inverse (double **Q, size_t n, size_t low, size_t high, double *scal) |
| | Обратное балансирование.
|
| void | eig_norm_Inf (double **Q, size_t n, double *wi) |
| | Нормирование собственных векторов.
|
| void | eig_vectors (double **A, size_t n, size_t low, size_t high, double *wr, double *wi, double **Q) |
| | Вычисление собственных векторов по методу обратной итерации.
|
В библиотеке реализованы следующие алгоритмы решения проблемы собственных значений:
| void eig_hess |
( |
double ** |
A, |
|
|
size_t |
n, |
|
|
size_t |
low, |
|
|
size_t |
high, |
|
|
double * |
wr, |
|
|
double * |
wi, |
|
|
int |
matq, |
|
|
double ** |
Q, |
|
|
size_t * |
iter, |
|
|
size_t * |
rc | |
|
) |
| | |
| void eig_jacobi |
( |
double ** |
A, |
|
|
size_t |
n, |
|
|
double * |
w, |
|
|
int |
matq, |
|
|
double ** |
Q, |
|
|
int * |
nrot, |
|
|
int * |
rc | |
|
) |
| | |
| void eig_tridiag |
( |
double * |
d, |
|
|
double * |
a, |
|
|
size_t |
n, |
|
|
int |
matq, |
|
|
double ** |
Q, |
|
|
size_t * |
rc | |
|
) |
| | |
Собственные числа симметричной трехдиагональной системы.
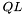 -алгоритм с неявными сдвигами для нахождения собственных векторов и собственных чисел действительной симметричной трехдиагональной матрицы
-алгоритм с неявными сдвигами для нахождения собственных векторов и собственных чисел действительной симметричной трехдиагональной матрицы  . Матрица
. Матрица  может быть получена с помощью функции eig_tridiag_reduction. На входе
может быть получена с помощью функции eig_tridiag_reduction. На входе 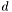 содержит диагональ матрицы
содержит диагональ матрицы  , на выходе - собственные числа Вектор
, на выходе - собственные числа Вектор 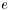 на входе содержит поддиагональ матрицы
на входе содержит поддиагональ матрицы  , на выходе вектор теряет свои значения.
, на выходе вектор теряет свои значения.
Если 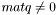 , то ищутся также собственные векторы. Если необходимы собственные векторы трехдиагональной матрицы, то матрица
, то ищутся также собственные векторы. Если необходимы собственные векторы трехдиагональной матрицы, то матрица 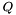 на входе должна быть единичной. Если нужно найти собственные векторы матрицы, к которой уже применяли функцию eig_tridiag_reduction, то
на входе должна быть единичной. Если нужно найти собственные векторы матрицы, к которой уже применяли функцию eig_tridiag_reduction, то 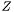 должна быть матрицей, возвращаемой функцией eig_tridiag_reduction. В обоих случаях
должна быть матрицей, возвращаемой функцией eig_tridiag_reduction. В обоих случаях 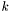 -й столбец возвращаемой матрицы
-й столбец возвращаемой матрицы 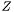 есть нормированный собственный вектор, соответствующий собственному числу
есть нормированный собственный вектор, соответствующий собственному числу ![$d[k]$](form_467.png) . Если собственные векторы не нужны, то нужно положить
. Если собственные векторы не нужны, то нужно положить 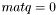 . В этом случае
. В этом случае 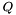 не используется и может быть равной
не используется и может быть равной 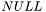 .
.
Если 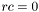 , то вычисление успешное, иначе на вычисление одного из собственных чисел было потрачено более
, то вычисление успешное, иначе на вычисление одного из собственных чисел было потрачено более 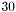 итераций. В этом случае
итераций. В этом случае 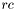 возвращает количество верно найденных собственных чисел (и векторов).
возвращает количество верно найденных собственных чисел (и векторов).
- Примеры:
-
xeigsym.c.
| void eig_tridiag_reduction |
( |
double ** |
A, |
|
|
size_t |
n, |
|
|
int |
matq, |
|
|
double * |
d, |
|
|
double * |
a | |
|
) |
| | |
 --- квадратная матрица. Собственным вектором называется такой ненулевой вектор
--- квадратная матрица. Собственным вектором называется такой ненулевой вектор 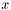 , что
, что 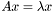 для некоторого числа
для некоторого числа 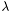 . При этом
. При этом 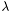 называется собственным значением (или собственным числом). Проблема собственных значений заключается в нахождении части (или всех) собственных значений и (если требуется) соответствующих им собственных векторов.
называется собственным значением (или собственным числом). Проблема собственных значений заключается в нахождении части (или всех) собственных значений и (если требуется) соответствующих им собственных векторов. -алгоритм для симметричной вещественной матрицы. Вначале с помощью функции
-алгоритм для симметричной вещественной матрицы. Вначале с помощью функции 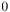 . Затем применятся
. Затем применятся 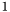 . Строки с нулями вне диагонали имеют номера с
. Строки с нулями вне диагонали имеют номера с 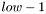 и
и 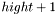 по
по 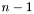 . Элементы вектора
. Элементы вектора 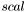 на этих позициях равны соответствующим собственным векторам, на остальных позициях --- соответствующим масштабным множителям.
на этих позициях равны соответствующим собственным векторам, на остальных позициях --- соответствующим масштабным множителям. 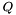 , найденным для сбалансированной матрицы
, найденным для сбалансированной матрицы 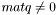 , - собственные векторы. Действительные части собственных чисел возвращаются в векторе
, - собственные векторы. Действительные части собственных чисел возвращаются в векторе 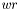 , мнимые ---
, мнимые --- 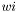 . Для вещественных собственных чисел (
. Для вещественных собственных чисел (![$wi[j]=0$](form_478.png) ) столбец
) столбец 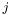 содержит соответствующий собственный вектор. Для пары комплексно сопряженных собственных чисел (
содержит соответствующий собственный вектор. Для пары комплексно сопряженных собственных чисел (![$wr[j]=wr[j+1]$](form_479.png) ,
, ![$wi[j]=-wi[j+1]$](form_480.png) )
) 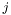 -й столбец матрицы
-й столбец матрицы 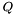 содержит действительную часть
содержит действительную часть 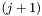 -й - его мнимую часть.
-й - его мнимую часть. 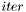 возвращается число итераций, используемых для нахождения каждого собственного числа.
возвращается число итераций, используемых для нахождения каждого собственного числа.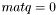 , то на место матрицы
, то на место матрицы 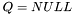 .
.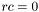 . В противном случае число итераций превысило 30 и в
. В противном случае число итераций превысило 30 и в 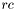 возвращается количество верно найденных собственных чисел.
возвращается количество верно найденных собственных чисел.  методом вращений Хаусхолдера приводится к верхней форме Хессенберга. На выходе элементы верхнего треугольника и поддиагонали матрицы
методом вращений Хаусхолдера приводится к верхней форме Хессенберга. На выходе элементы верхнего треугольника и поддиагонали матрицы 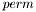 --- вектор перестановок --- в дальнейшем используется функцией elmtrans
--- вектор перестановок --- в дальнейшем используется функцией elmtrans 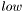 ,
, 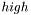 --- из функции
--- из функции 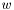 возвращаются собственные числа. Если на входе
возвращаются собственные числа. Если на входе 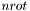 возвращает число использованных вращений Якоби.
возвращает число использованных вращений Якоби.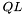 -алгоритм с неявными сдвигами для нахождения собственных векторов и собственных чисел действительной симметричной трехдиагональной матрицы
-алгоритм с неявными сдвигами для нахождения собственных векторов и собственных чисел действительной симметричной трехдиагональной матрицы 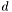 содержит диагональ матрицы
содержит диагональ матрицы 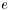 на входе содержит поддиагональ матрицы
на входе содержит поддиагональ матрицы 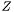 должна быть матрицей, возвращаемой функцией
должна быть матрицей, возвращаемой функцией 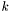 -й столбец возвращаемой матрицы
-й столбец возвращаемой матрицы ![$d[k]$](form_467.png) . Если собственные векторы не нужны, то нужно положить
. Если собственные векторы не нужны, то нужно положить 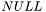 .
.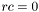 , то вычисление успешное, иначе на вычисление одного из собственных чисел было потрачено более
, то вычисление успешное, иначе на вычисление одного из собственных чисел было потрачено более 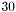 итераций. В этом случае
итераций. В этом случае 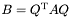 .
. 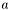 --- поддиагональные элементы,
--- поддиагональные элементы, ![$a[0] = 0$](form_503.png) . Если
. Если  1.4.7
1.4.7