Функции
 -разложение ленточной системы.
-разложение ленточной системы.  -разложения.
-разложения.
Функции | |
| void | band_tridiag (double *a, double *d, double *c, double *b, double *x, size_t n) |
| Решение трехдиагональной системы методом прогонки. | |
| void | band_mult_col (double **A, size_t n, size_t m1, size_t m2, double *b, double *c) |
| Умножение ленточной матрицы на плотный столбец. | |
| void | band_decomp (double **A, size_t n, size_t m1, size_t m2, double **L, size_t *p, int *sgn) |
 -разложение ленточной системы. -разложение ленточной системы. | |
| void | band_solve (double **A, size_t n, size_t m1, size_t m2, double **L, size_t *p, double *b) |
Решение ленточной системы на основе ее  -разложения. -разложения. | |
Файл содержит функции для работы с ленточными матрицами.
Матрица  с элементами
с элементами 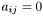 при
при 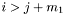 или
или 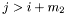 называется ленточной. Величина
называется ленточной. Величина 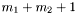 называется шириной ленты, а
называется шириной ленты, а 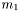 и
и 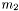 - шириной нижней полуленты и шириной верхней полуленты соответственно. При
- шириной нижней полуленты и шириной верхней полуленты соответственно. При 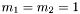 получаем трехдиагональную матрицу. Элементы
получаем трехдиагональную матрицу. Элементы 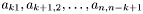 называются
называются 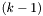 -й поддиагональю, а
-й поддиагональю, а 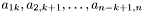 -
- 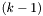 -й наддиагональю.
-й наддиагональю.
Для хранения элементов ленточной матрицы используется компактная схема. Ленточной матрице  поставим в соответствие матрицу
поставим в соответствие матрицу 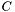 размера
размера 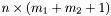 с элементами
с элементами 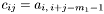 , которую и будем хранить в двумерном массиве. Итак, каждому столбцу матрицы
, которую и будем хранить в двумерном массиве. Итак, каждому столбцу матрицы 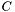 соответствует (под/над)диагональ матрицы
соответствует (под/над)диагональ матрицы  .
.
Подробности и примеры см. в [BelovZolotykh]
| void band_decomp | ( | double ** | A, | |
| size_t | n, | |||
| size_t | m1, | |||
| size_t | m2, | |||
| double ** | L, | |||
| size_t * | p, | |||
| int * | sgn | |||
| ) |
 -разложение ленточной системы.
-разложение ленточной системы.
Функция находит  -разложение
-разложение 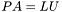 ленточной квадратной матрицы
ленточной квадратной матрицы  порядка
порядка  с шириной нижней полуленты
с шириной нижней полуленты 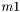 и шириной верхней полуленты
и шириной верхней полуленты 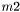 . Для хранения матрицы используется компактная схема. Элементы матрицы хранятся в массиве
. Для хранения матрицы используется компактная схема. Элементы матрицы хранятся в массиве  размера
размера 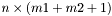 . Используется схема выбора главного элемента по столбцу. Элементы множителя
. Используется схема выбора главного элемента по столбцу. Элементы множителя 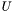 возвращаются в компактной форме в массиве
возвращаются в компактной форме в массиве  . Поддиагональные элементы множителя
. Поддиагональные элементы множителя 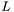 в компактной форме возвращаются в массиве
в компактной форме возвращаются в массиве 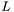 размера
размера 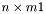 . Диагональные элементы матрицы
. Диагональные элементы матрицы 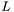 равны
равны 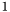 . Матрица перестановок
. Матрица перестановок 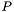 представлена вектором перестановок
представлена вектором перестановок 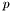 : на
: на 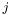 -й итерации
-й итерации 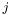 -я строка была переставлена с
-я строка была переставлена с ![$p[j]$](form_140.png) -й. На выходе
-й. На выходе 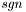 - определитель матрицы
- определитель матрицы 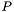 .
.
Трудоемкость:
| void band_mult_col | ( | double ** | A, | |
| size_t | n, | |||
| size_t | m1, | |||
| size_t | m2, | |||
| double * | b, | |||
| double * | c | |||
| ) |
Умножение ленточной матрицы на плотный столбец.
Ленточная матрица  , представленная схемой, описанной в описании band_decomp, умножается на вектор-столбец
, представленная схемой, описанной в описании band_decomp, умножается на вектор-столбец 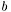 . Результат возвращается в массиве
. Результат возвращается в массиве 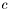 .
.
Трудоемкость:
| void band_solve | ( | double ** | A, | |
| size_t | n, | |||
| size_t | m1, | |||
| size_t | m2, | |||
| double ** | L, | |||
| size_t * | p, | |||
| double * | b | |||
| ) |
Решение ленточной системы на основе ее  -разложения.
-разложения.
Функция находит решение ленточной системы 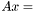 b на основе полученного функцией band_decomp
b на основе полученного функцией band_decomp  -разложения матрицы
-разложения матрицы  . На входе:
. На входе:
 ,
, 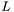 ,
, 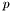 - массивы, возвращаемые функцией band_decomp,
- массивы, возвращаемые функцией band_decomp, ,
, 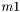 ,
, 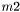 - порядок системы, ширина нижней и ширина верхней полулент соответственно.
- порядок системы, ширина нижней и ширина верхней полулент соответственно.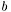 - правая часит системы уравнений.
- правая часит системы уравнений.
Решение записывается на месте вектора 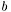 , остальные массивы не меняются и могут использоваться в дальнейшем для решения системы с другой правой частью.
, остальные массивы не меняются и могут использоваться в дальнейшем для решения системы с другой правой частью.
Трудоемкость:
| void band_tridiag | ( | double * | a, | |
| double * | d, | |||
| double * | c, | |||
| double * | b, | |||
| double * | x, | |||
| size_t | n | |||
| ) |
Решение трехдиагональной системы методом прогонки.
Решается трехдиагональная система порядка  . Массивы
. Массивы 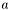 ,
, 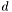 ,
, 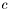 содержат коэффициенты системы, расположенные соответственно под главной диагональю, на ней и над ней. Элементы
содержат коэффициенты системы, расположенные соответственно под главной диагональю, на ней и над ней. Элементы ![$a[0]$](form_126.png) и
и ![$c[n-1]$](form_127.png) не используются. Массив
не используются. Массив 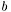 содержит правую часть системы. Решение возвращается в массиве
содержит правую часть системы. Решение возвращается в массиве 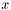 .
.
Трудоемкость: 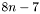
 1.4.7
1.4.7